什么叫做无限小数_什么叫做无限小数

(^人^) *** 次数：1999998 已用完，请联系开发者***

∪０∪ 圆周率能否算尽?与普朗克长度物体不可无限分割矛盾吗?这个问题颇具趣味性,首先来解答第一个问题:圆周率π是一个无穷无尽、永不重复的小数,它与进制无关。 数学领域中,我们把π称为无理数,意... π并没有什么神秘之处,每一个无理数背后都隐含着某种特定的几何关系。例如,一个单位边长的正方形,其对角线长度便是√2;又如,在60度的等...

把圆周率算下去有啥意义?科学家解释让人恍然大悟面对这个无限但是又有价值的小数π数,像我们这些非数学专业出身的人想深究却实在是无从下手,无法理解π的无限小数位数中到底隐藏着怎样的价值。而在我国有一位科学家对这一点进行了解释,让人们终于深刻地理解了把圆周率继续算下去的意义是什么? 一、π的应用领域。 明代数...

圆周率π能被算尽吗?算尽了会怎样?圆周率π,我们都知道它是一个无理数。何为无理数?就是无限不循环小数,既然是无限不循环,当然是不可能被完全算出来的,不可能用小数准确... 这说明什么?说明了一个无限的概念,圆的周长永远会无限地逼近一个值,但是永远到不了这个值,也就是说不存在真正意义上的圆。 人类历史上...

╯＾╰〉

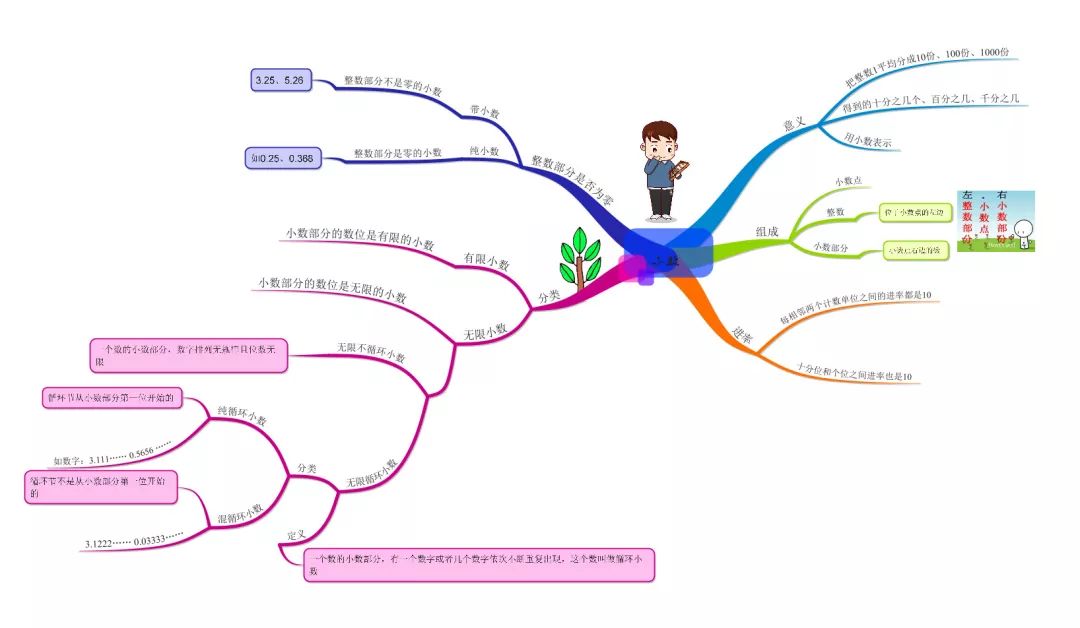
⊙０⊙ 2022—2023学年五年级上册数学第三至四单元练习资料解析这份2022—2023学年五年级上册数学第三至四单元的练习资料,涵盖的数学知识丰富,题型也多种多样。从知识层面来讲,其中涉及小数除法运算,比如商的变化规律以及小数除法的具体计算;还有循环小数、有限小数和无限小数的认知与区分;另外,可能性相关知识,像判断事件发生可能性的...

∩＾∩

圆周率的尽头:普朗克长度与无限分割之谜这个问题颇具趣味性,首先来解答第一个问题:圆周率π是一个无穷无尽、永不重复的小数,它与进制无关。 在数学领域中,我们把π称为无理数,... π并没有什么神秘之处;每一个无理数背后都隐藏着某种特定的几何关系。例如,在一个单位边长的正方形中,其对角线长度便是√2;而在60度的...

圆周率之谜:普朗克长度揭示的无限分割悖论这个问题颇具趣味性,首先来解答第一个问题:圆周率π是一个无穷无尽、永不重复的小数,它与进制无关。 在数学领域中,我们把π称为无理数,... π并没有什么神秘之处,每一个无理数背后都隐含着某种特定的几何关系。例如,一个单位边长的正方形,其对角线长度便是√2;又如,在60度的等...

ˇωˇ 一米长物体能否完美三等分?揭秘1/3的无限奥妙!无理数与有理数之间的差异其实非常简单:它们是无限不循环的小数,仅此而已。 我们不能因为一个数是无限不循环的就对它另眼看待,更不能潜意识地认定“无限不循环的数就不是确定的数”。 许多人总是情不自禁地想要把无理数以小数形式完全表达出来,如果不这样做,他们就会觉得心...

∩▽∩ 五年级上册数学第三四单元练习题这份 2022—2023 学年五年级上册数学第三至四单元练习资料,涵盖了丰富的数学知识与多种题型。从知识内容看,包含小数除法的运算,像商的变化规律、小数除法的计算;循环小数、有限小数、无限小数的认识与区分;还有可能性的相关知识,如事件发生的可能性大小判断等。题型方面,有...

圆周率的尽头在哪里?普朗克长度揭示物质分割极限,是悖论还是真相?这个问题颇具趣味性,首先来解答第一个问题:圆周率π是一个无穷无尽、永不重复的小数,它与进制无关。 在数学领域,我们将π称为无理数,这... π并没有什么神秘之处,每一个无理数背后都隐含着某种特定的几何关系。例如,一个单位边长的正方形,其对角线长度便是√2;又如,在60度的等...

(#｀′)凸 圆周率的尽头在哪里?普朗克长度揭示的极限,是科学的终点还是起点?这个问题颇具趣味性,首先来解答第一个问题:圆周率π是一个无穷无尽、永不重复的小数,它与进制无关。 在数学领域中,我们把π称为无理数,... π并没有什么神秘之处,每一个无理数背后都隐含着某种特定的几何关系。例如,一个单位边长的正方形,其对角线长度便是√2;又如,在60度的等...